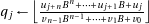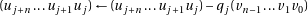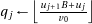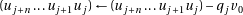On integer division
1 Integer division
The integer division of an integer  , the dividend, by another non nul integer
, the dividend, by another non nul integer  , the divisor, is the
determination of two integers: the quotient
, the divisor, is the
determination of two integers: the quotient 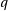 and the remainder
and the remainder  such that
such that 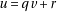 and
and
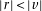 . With this definition, there are two results if
. With this definition, there are two results if  is not a divisor of
is not a divisor of  . To make the result unique,
one has to impose an additional condition.
. To make the result unique,
one has to impose an additional condition.
Three such conditions are in use. But first a word about the notations used in this document. 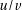 is
the real division of
is
the real division of  by
by  . When an uniquifying condition is implied by the context,
. When an uniquifying condition is implied by the context, 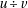 is the
quotient and
is the
quotient and 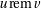 is the remainder of an integer division. When the uniquifying condition is not
important
is the remainder of an integer division. When the uniquifying condition is not
important 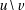 is the quotient and
is the quotient and 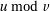 is the remainder.
is the remainder.
When defining the uniquifying conditions, we’ll also make use the two functions:

1.1 Truncating division
The truncating division can be defined in two equivalent ways: one relating the value of  with the
result of the real division (which explains the name we use), the other binding the sign of
with the
result of the real division (which explains the name we use), the other binding the sign of  with the
sign of the dividend:
with the
sign of the dividend:
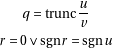
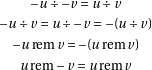
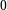 ; for the quotient, they are the same one that
the real division has. These symmetries implies that
; for the quotient, they are the same one that
the real division has. These symmetries implies that 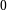 is special (for instance, there are
is special (for instance, there are
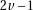 integers giving
integers giving  when divided by
when divided by  when there are only
when there are only  such integers for other
quotients).
such integers for other
quotients).
1.2 Floor division
Again, two equivalent ways of defining the division:
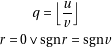
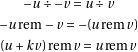
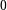 is now
behaving like other numbers.
is now
behaving like other numbers.
1.3 Positive remainder division
There is only one condition to define this division:
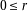
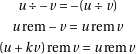
To illustrate, here are some examples:
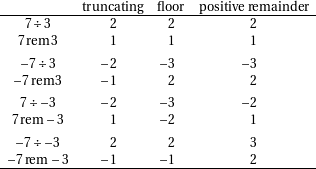 |
Mathematicians tend to define the version they want before using it if it is important. Programmers often don’t have that luxery and have to make with what the system they use provides them. It happens that processors and languages seem to have standardized on the floor division even if the other two (they differ only for negative dividend, which seems rare) appear to be more in use among the mathematicians. Exceptions exist, some languages even provides two remainders (the truncating and the floor one).
Going from one version to the other isn’t difficult, but it can be tedious. It is just adding or substracting one to the quotient, and adding or substracting the divisor to the remainder depending on the sign of the dividend and the divisor. As an example, here is an algorithm computing the floor division assuming that the truncating one is available (in practice the most common case):
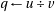
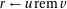
if
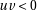 then
then  Doing
Doing 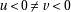 may be preferable as it will not overflow.
may be preferable as it will not overflow. 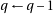
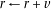
end if
2 Long division
In this section, we’ll see how to divide a  digit number
digit number  whose digits in some base
whose digits in some base 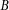 are
are
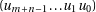 by a
by a  digits number
digits number  whose digits are
whose digits are 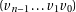 using only numbers less
that
using only numbers less
that 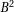 .
.
The algorithm we’ll use is the long division, the pencil and paper method by which we have learned
how to do division. We’ll consider that there is an additional digit for  :
: 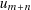 , currently its value is
, currently its value is 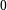 and it just helps to take into account to fact that such division sometimes produces
and it just helps to take into account to fact that such division sometimes produces  digits and
sometimes
digits and
sometimes 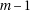 ; it will be needed in the final version of the algorithm anyway. The algorithm is thus
the following:
; it will be needed in the final version of the algorithm anyway. The algorithm is thus
the following:
At the end, 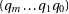 is the quotient and the remainder is
is the quotient and the remainder is 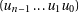 .
.
The only difficulty in applying this algorithm is getting the next digit:
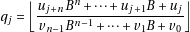
for which we known that 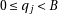 .
.
Well, it is easy to do it if 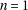 :
:
In the other cases, as we are using numbers less that 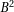 , the obvious idea is the use
, the obvious idea is the use
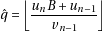 |
(we are temporarily dropping the  indices). Let’s try to find out how near we are from the true value.
First we deduce:
indices). Let’s try to find out how near we are from the true value.
First we deduce:
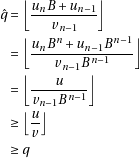
Then bound out the other direction:
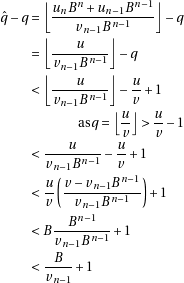
so if 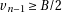 then
then 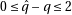 . Knuth [1, section 4.3.1] using
. Knuth [1, section 4.3.1] using
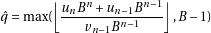
shows that then 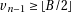 is sufficient.
is sufficient.
In order to tighen our bound on 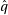 , let’s try to impose
, let’s try to impose 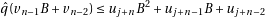 :
:
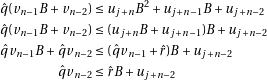
This last condition can be computed without overflow if 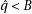 and
and 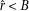 (if it isn’t, the condition is
false).
(if it isn’t, the condition is
false).
We’ll then have
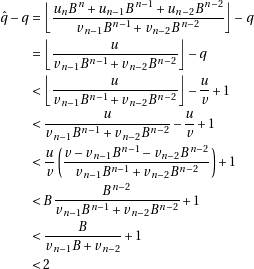
If one consider that 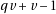 can differ of
can differ of 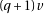 only in the last digit, one see that to be more
precise, one need to take all the digits into account.
only in the last digit, one see that to be more
precise, one need to take all the digits into account.
Let’s modify our initial algorithm using the above properties. To take advantage of the fact that if
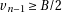 then
then 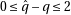 , we’ll multiply both dividend and divisor by
, we’ll multiply both dividend and divisor by 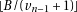 (the
dividend will need the additional digit we have already introduced, the divisor won’t need another digit,
but its first digit will be
(the
dividend will need the additional digit we have already introduced, the divisor won’t need another digit,
but its first digit will be 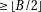 ) and divide the remainder by the same value at the end. We’ll
first use
) and divide the remainder by the same value at the end. We’ll
first use 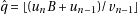 then adjust
then adjust 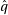 until
until 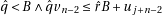 (the
condition in the algorithm is a little more complicated in order to prevent overflow). Then we are
sure that
(the
condition in the algorithm is a little more complicated in order to prevent overflow). Then we are
sure that 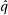 is at most one too big, so after having subtracted
is at most one too big, so after having subtracted 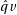 from
from 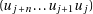 we check if the result had a borrow and add back
we check if the result had a borrow and add back  in that case. The result is algorithm
4.
in that case. The result is algorithm
4.
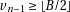 .
. 2:
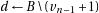
3: if
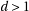 then
then 4:
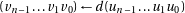
5:
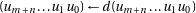
6: end if
7: Now determine each digits.
8: for
 do
do 9: Get our estimate
10:
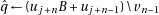
11:
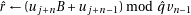
12: Refine if needed
13: while
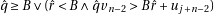 do
do 14:
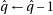
15:
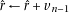
16: end while
17: Do the substraction
18:
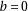
19: for
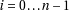 do
do 20:
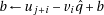
21:
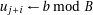
22:
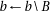
23: end for
24: If there is a borrow, that mean the refinement wasn’t enough to get it right, add back
 and adjust
and adjust 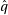 .
. 25: if
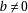 then
then 26:
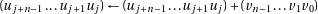
27:
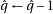
28: end if
29:
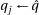
30: end for
31: Finally undo the adjustment of the remainder
32: if
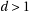 then
then 33:
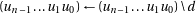
 Use algorithm 3
Use algorithm 3 34: end if
For 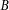 even
even 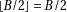 , the refinement loop will be executed at most twice, so unrolling the loop
should be considered in an implementation.
, the refinement loop will be executed at most twice, so unrolling the loop
should be considered in an implementation.
With 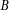 odd, it is possible to get
odd, it is possible to get 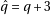 (for example
(for example 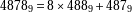 and
and
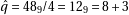 ). But as the additional condition we use to ensure
). But as the additional condition we use to ensure 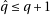 doesn’t depend
on
doesn’t depend
on 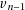 , unrolling the loop twice would be enough, the add back step will handle final
adjustment.
, unrolling the loop twice would be enough, the add back step will handle final
adjustment.
References